How To Find The Slant Height Of A Frustum Pyramid

If a pyramid is cut through by a plane parallel to its base, the portion of the pyramid betwixt that plane and the base is called the frustum of the pyramid.

The Volume of the Frustum of a Pyramid

A general formula for the volume of any pyramid tin be derived in terms of the areas of the 2 bases and the height of the frustum.

Consider any frustum of a pyramid $$KE$$ in the effigy with the lower base $${A_1}$$, upper base $${A_2}$$ and the altitude $$h$$. Complete the pyramid $$O – Hard disk$$ of which the frustum $$KE$$ is a role.

Denoted by $$p$$, the volume of the small pyramid $$O – QM$$ whose altitude is $$a$$. And then the altitude of $$O – Hd$$ is $$a + h$$.

Let $$Five$$ and $$P$$ correspond the book of the frustum $$KE$$ and the pyramid $$O – HD$$, respectively.

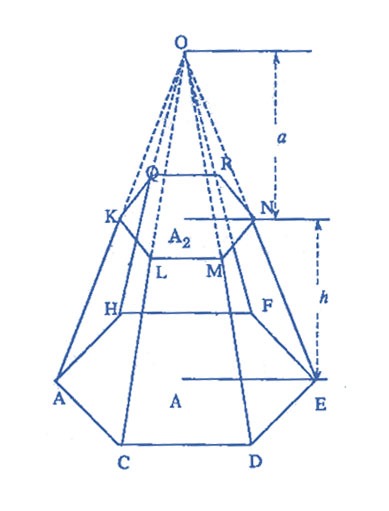
$$\therefore $$ from the effigy it is easily seen that $$5 = P – p$$. Expressing this equality in terms of the dimensions, we may write:

\[\brainstorm{gathered} V = \frac{i}{3}{A_1}\left( {h + a} \right) – \frac{1}{3}{A_2}a = \frac{ane}{3}\left[ {{A_1}h + {A_1}a – {A_2}a} \right] \\ \Rightarrow V = \frac{i}{three}\left[ {{A_1}h + a\left( {{A_1} – {A_2}} \right)} \correct]\, – – – \left( i \right) \\ \terminate{gathered}\]

The pyramid $$O – HD$$ may exist considered every bit cut by the ii parallel planes $$Hard disk drive$$ and $$QM$$.

Hence
\[\frac{{{a^2}}}{{{{\left( {h + a} \right)}^2}}} = \frac{{{A_2}}}{{{A_1}}}\]

(If a pyramid is cut by two parallel planes, the areas of the sections are proportional to the squares of their distances from the vertex.)

Taking the square root of both sides, we accept
\[\brainstorm{gathered} \frac{a}{{h + a}} = \frac{{\sqrt {{A_2}} }}{{\sqrt {{A_1}} }} \\ \Rightarrow a\sqrt {{A_1}} = h\sqrt {{A_2}} + a\sqrt {{A_2}} \\ \terminate{gathered} \]

Transposing $$a\sqrt {{A_2}} $$ to the Fifty.H.S. of this equation and factorizing,

\[\brainstorm{gathered} a\left( {\sqrt {{A_1}} – \sqrt {{A_2}} } \right) = h\sqrt {{A_2}} \\ \Rightarrow a = \frac{{h\sqrt {{A_2}} }}{{\sqrt {{A_1}} – \sqrt {{A_2}} }} \\ \stop{gathered} \]

Substituting the value of $$a$$ in (1), we take

\[\begin{gathered} V = \frac{1}{3}\left[ {{A_1}h + \frac{{h\sqrt {{A_2}} }}{{\sqrt {{A_1}} – \sqrt {{A_2}} }}\left( {{A_1} – {A_2}} \right)} \correct] \\ \Rightarrow V = \frac{1}{iii}\left[ {{A_1}h + \frac{{h\sqrt {{A_2}} }}{{\sqrt {{A_1}} – \sqrt {{A_2}} }}\left( {{A_1} + {A_2}} \right)\left( {{A_1} – {A_2}} \right)} \right] \\ \Rightarrow 5 = \frac{ane}{iii}\left[ {{A_1}h + h\sqrt {{A_2}} \left( {{A_1} + {A_2}} \correct)} \correct] \\ \Rightarrow 5 = \frac{one}{3}\left[ {{A_1}h + h\sqrt {{A_1}{A_2}} + {A_2}h} \correct] = \frac{1}{three}h\left[ {{A_1} + {A_2} + \sqrt {{A_1}{A_2}} } \right] \\ \end{gathered} \]

i.e. the volume of a frustum of a pyramid is equal to one-third the production of the altitude and the sum of the upper base of operations, the lower base and the foursquare root of the product of the 2 bases.

The Lateral Surface Surface area of the Frustum of a Pyramid

Each of the faces, such equally $$CDML$$, of the frustum of a pyramid is a trapezium, and the area of each trapezium will be half the sum of the parallel sides, $$CD$$ and $$ML$$, multiplied past the slant altitude betwixt them.

In the frustum of pyramid on a square base, permit $$a$$ denote the length of each side of the base of operations, $$b$$ the length of each side of the other stop, and $$l$$ the height of the frustum.

Each face up $$CDML$$ is a trapezium, and the lengths of the parallel sides are $$a$$ and$$b$$.
\[\begin{gathered} {\text{Area}}\,{\text{CDML}} = \frac{1}{2}\left( {a + b} \right)l \\ Lateral\,area = \frac{1}{ii}\,\left( {sum\,of\,perimeters\,of\,bases \times slant\,summit} \right) \\ \stop{gathered} \]

Case :

A frustum of a pyramid has rectangular ends, and the sides of the base are25dm and 36dm. If the area of the peak face is 784sq.dm and the meridian of the frustum is 60dm, find its book.

Solution :

Here

$${A_1} = 25 \times 36 = 900\,{\text{sq}}{\text{.dm}}$$, $${A_2} = 784\,{\text{sq}}{\text{.dm}}$$ \[\begin{gathered} V = \frac{1}{iii}h\left[ {{A_1} + {A_2} + \sqrt {{A_1}{A_2}} } \right] = \frac{1}{three} \times 60\left[ {900 + 784 + \sqrt {900 \times 784} } \correct] \\ V = 20 \times \left( {1684 + 840} \correct) = 20 \times 2524 = 50480\,{\text{sq}}{\text{.}}\,{\text{dm}} \\ \stop{gathered} \]